Matthew 2
Matthew's gospel moves very quickly from Jesus's genealogy, a few paragraphs about his birth (compared to Luke who spends two chapters there) and straight on to the visit of the Magi, then Herod's plans to find and kill Jesus.
Verses 22-23 of Matthew 1 reads, "All this took place to fulfill what the Lord had said through the prophet 'The virgin will conceive and give birth to a son, and they will call him Immanuel'(which means “God with us”)." This is a recurring theme throughout Matthew's gospel; he constantly points to the Old Testament prophecies about the Messiah, and then shows that Jesus was fulfilling them. The phrase, "this took place to fulfill the prophecy.." or similar, occurs once in Matthew 1 (not including the entire genealogy, which we saw last time is a great long list of fulfilled promises) and three times in Matthew 2, and that's just for starters!
In Matthew 2 we get political refugees and infant genocide. We wouldn't normally call it that, because it's all couched safely in different words than that, but that's what it comes down to. Joseph and Mary have to flee to Egypt with Jesus, to avoid the slaughter of all young boys that was ordered by a paranoid Herod.
Matthew 2 is a short chapter, just 21 verses, and most of it is very well known. It's straight-forward enough, but one question I have is why go to Egypt? Why not forget about the whole incident, or perhaps God could have directed the wise men directly to Bethlehem instead of to King Herod? There are parallels with Moses, who led the people out of Egypt and into the Promised Land, which could well be what Matthew is highlighting here.
I should mention at this point that Luke's gospel doesn't have the 'flight to Egypt', but Matthew and Luke aren't contradicting each other - it's just that they're highlighting certain events. Luke doesn't feel it's relevant to include the flight to Egypt, but Matthew does, for other reasons. Matthew is aiming throughout his gospel to highlight how Jesus was foretold in the Old Testament, and the parallels with other Old Testament characters help him to support and highlight this point.
Mostly my experiences with web analytics and online testing; some maths, some opinions, and the occasional Chess game.
Header tag
Thursday 9 February 2012
Tuesday 7 February 2012
Puzzle: Snakes and Ladders
(also known as the Collatz conjecture, or Syracuse problem)
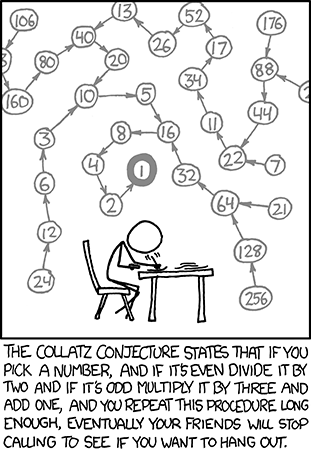
Courtesy of Calculator Fun and Games, which first introduced me to it, here's an interesting puzzle that is easy enough to understand, but which has developed into a far more complicated problem. In fact, if you want to make the easy idea hard to understand, just go and read the Wikipedia entry - it is far too complicated, as much of maths on Wikipedia tends to be.
Anyway, here it is: Take a number - any number. If it's odd, multiply by three and add one. If it's even, divide by two. Now take your new number and follow the same process - odd numbers multiply by three and add one, even numbers divide by two. And so on, and so on.
What do you find? And, more importantly, does this always happen?
Let's try a few numbers:
35 is odd, so multiply by 3 ( = 105) and then add 1 = 106
106 is even, so divide by 2 = 53
53 is odd, so multiply by 3 (=159) and then add 1 = 160
160 is even, so divide by 2 = 80
80 is even, so divide by 2 = 40
40 is even, so divide by 2 = 20
20 is even, so divide by 2 = 10
10 is even, so divide by 2 = 5
5 is odd so multiply by 3 and add 1 = 16
16 is even, divide by 2 = 8, which is also even, divide by 2 = 4, then 2, then 1.
If (or should that be "When"?) you reach 1, then you stop. Otherwise, you get stuck in a loop that goes 1 -- 4 -- 2 -- 1 -- 4 -- 2 etc.
The question is: Do you always reach 1? Is there a number out there somewhere that doesn't eventually drop down to 1?
The path length for numbers (how long it takes for a number to reach 1) is not predictable - certainly not easily, as far as I know, and so there's much research there as well.
For example, 26 follows the path 26 - 13 - 40 - 20 - 10 - 5 - 17 - 8 - 4 - 2 - 1
But 27 follows a completely different path...
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077,9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
...with its highest point at over 9,000! All in all, it has 111 steps in its path to 1.
Here are the paths for all the numbers 1-20 (and the numbers that they include):
There are various puzzles connected with this problem. The main one is to prove that all paths end at 1, but that's still not been completely solved yet, and some of mathematics' greatest minds are having a go.
A good alternative, though, is to find the longest path possible for three-digit and four-digit figures. I'm not sure if it's a puzzle, or a game, and if it's a game, then I figure it'd probably spoil it for you to know the answer before you start :-)
Courtesy of Calculator Fun and Games, which first introduced me to it, here's an interesting puzzle that is easy enough to understand, but which has developed into a far more complicated problem. In fact, if you want to make the easy idea hard to understand, just go and read the Wikipedia entry - it is far too complicated, as much of maths on Wikipedia tends to be.
Anyway, here it is: Take a number - any number. If it's odd, multiply by three and add one. If it's even, divide by two. Now take your new number and follow the same process - odd numbers multiply by three and add one, even numbers divide by two. And so on, and so on.
What do you find? And, more importantly, does this always happen?
Let's try a few numbers:
35 is odd, so multiply by 3 ( = 105) and then add 1 = 106
106 is even, so divide by 2 = 53
53 is odd, so multiply by 3 (=159) and then add 1 = 160
160 is even, so divide by 2 = 80
80 is even, so divide by 2 = 40
40 is even, so divide by 2 = 20
20 is even, so divide by 2 = 10
10 is even, so divide by 2 = 5
5 is odd so multiply by 3 and add 1 = 16
16 is even, divide by 2 = 8, which is also even, divide by 2 = 4, then 2, then 1.
If (or should that be "When"?) you reach 1, then you stop. Otherwise, you get stuck in a loop that goes 1 -- 4 -- 2 -- 1 -- 4 -- 2 etc.
The question is: Do you always reach 1? Is there a number out there somewhere that doesn't eventually drop down to 1?
The path length for numbers (how long it takes for a number to reach 1) is not predictable - certainly not easily, as far as I know, and so there's much research there as well.
For example, 26 follows the path 26 - 13 - 40 - 20 - 10 - 5 - 17 - 8 - 4 - 2 - 1
But 27 follows a completely different path...
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077,9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
...with its highest point at over 9,000! All in all, it has 111 steps in its path to 1.
 |
| Image from Calculator Fun and Games (original was black and white line drawing) |
 |
| Image from: "Professor Stewart's Hoard of Mathematical Treasures" |
A good alternative, though, is to find the longest path possible for three-digit and four-digit figures. I'm not sure if it's a puzzle, or a game, and if it's a game, then I figure it'd probably spoil it for you to know the answer before you start :-)
Labels:
collatz conjecture,
maths,
problem,
puzzle
Monday 6 February 2012
Puzzle: Magic Square
I'm not entirely sure if this puzzle already has a name... it probably does, but I haven't found it. I think it's probably fair to call it a magic square, since the idea is to use a set of numbers in a square to achieve the same total in the rows, columns and long diagonals. The difference here is that the numbers are four sets of the numbers 1-4, in four different colours (white, grey, black and yellow), and there's an additional condition that no row, column or long diagonal must have a colour repeated.
To make it easier to explain, here is a set of blocks, showing the four digits 1-4 in their four colours (sixteen blocks in total).
There are a number of comments I'd like to make on this solution, but before I do, I'd like to introduce (or re-introduce, if you've seen it before) a distance that I call the knight-move. In Chess, the knight moves by going one square forwards, backwards, or left or right, followed by two squares left, right, or backwards or forwards (at 90o to the original direction) . Again, it's easier to show with a diagram, so here goes:
The same applies for any of the other numbers, for example, the 2s start from the bottom right. The whole solution has rotational symmetry - if you imagine moving the grid around by a quarter turn, then you find the same solution for a different number (1, 4 , 2, 3 in this example).
The same also applies for the coloured numbers - in the next diagram I've highlighted the white numbers. Starting in the lower right corner with 2, the white numbers are all connected by knight-moves (one across and two up, or two across and one down, etc).
Notice here that one knight move from the white 2 gives the white sequence (shown above), while the other knight move from that 2 gives the sequence for all the other 2s.
So, whenever you encounter any puzzle of the form, "Put the objects into the grid so that each row and column only contains one of each type of object" - whether it's numbers, letters, or shapes, remember the knight-move as a short cut towards the solution!
To make it easier to explain, here is a set of blocks, showing the four digits 1-4 in their four colours (sixteen blocks in total).
There are a number of solutions to this puzzle, and I have no intention of calculating the number. Instead, I'm going to look at an example solution, and discuss my thoughts on it, so that - hopefully - you'll be able to solve similar problems in the future.
I was going to insert a few line breaks here, just in case you're included to try and solve the problem without the solution.
However, I suspect the answer is complicated enough that you won't solve it just by glancing at the answer!
Here's one solution, then:
There are a number of comments I'd like to make on this solution, but before I do, I'd like to introduce (or re-introduce, if you've seen it before) a distance that I call the knight-move. In Chess, the knight moves by going one square forwards, backwards, or left or right, followed by two squares left, right, or backwards or forwards (at 90o to the original direction) . Again, it's easier to show with a diagram, so here goes:
This motif shows up a number of times in the magic square puzzle here, and in many other puzzles of the type, "Arrange the numbers so that such-and-such don't appear in the same row or column." Let's look at the solution again; firstly, here are all the 4s.
Can you see how the 4s are all connected by a knight-move, starting from the four in the top corner? The sequence grey-yellow-white-black is a series of three knight-moves.
The same applies for any of the other numbers, for example, the 2s start from the bottom right. The whole solution has rotational symmetry - if you imagine moving the grid around by a quarter turn, then you find the same solution for a different number (1, 4 , 2, 3 in this example).
The same also applies for the coloured numbers - in the next diagram I've highlighted the white numbers. Starting in the lower right corner with 2, the white numbers are all connected by knight-moves (one across and two up, or two across and one down, etc).
Notice here that one knight move from the white 2 gives the white sequence (shown above), while the other knight move from that 2 gives the sequence for all the other 2s.
So, whenever you encounter any puzzle of the form, "Put the objects into the grid so that each row and column only contains one of each type of object" - whether it's numbers, letters, or shapes, remember the knight-move as a short cut towards the solution!
Sunday 5 February 2012
Word 3:45 One: Matthew 1
Matthew 1
Matthew begins his gospel with the ancestry of Jesus, all the way back to Abraham. For a Jew, it was very important that they could demonstrate they were one of Abraham's descendants, and were therefore thoroughbred Jews. We'll see this frequently in Matthew's gospel.
Most people reading Matthew 1 today don't see the relevance - even taking into consideration that Matthew was demonstrating Jesus' validity as a Jew. However, Matthew was also demonstrating a key point: God always keeps His promises. God had made promises to a number of people in the Old Testament, that one day, their descendant would be the Messiah.
Let's look at a few examples:
Abraham
Judah
Genesis 49:8-10
"Judah, your brothers will praise you; your hand will be on the neck of your enemies;
your father’s sons will bow down to you.
You are a lion’s cub, Judah; you return from the prey, my son.
Like a lion he crouches and lies down, like a lioness—who dares to rouse him?
The sceptre [a symbol of royalty] will not depart from Judah,
nor the ruler’s staff from between his feet, until he to whom it belongs shall come"
David
2 Samuel 7:16
"Your house and your kingdom will endure forever before me; your throne will be established forever."
And another more obscure member of Jesus' ancestors:
Zerubbabel (Matthew 1:12. Zerubbabel led the work on the reconstruction of Jerusalem from the rubble that was left when the Israelites returned from their exile)
Haggai 2:20-23
20 The word of the LORD came to Haggai a second time on the twenty-fourth day of the month: 21“Tell Zerubbabel governor of Judah that I am going to shake the heavens and the earth. 22 I will overturn royal thrones and shatter the power of the foreign kingdoms. I will overthrow chariots and their drivers; horses and their riders will fall, each by the sword of his brother.
The signet ring in Old Testament times was a royal symbol. A signet, engraved with the king's seal, was used to endorse official documents. To guard against misuse, the king wore it as a ring or on a necklace. God declares here that He's chosen Zerubbabel and would keep him safe to fulfil his appointed purpose; since this didn't happen during his lifetime, we can see that this would extend to one of his descendants... and sure enough...
Matthew begins his gospel with the ancestry of Jesus, all the way back to Abraham. For a Jew, it was very important that they could demonstrate they were one of Abraham's descendants, and were therefore thoroughbred Jews. We'll see this frequently in Matthew's gospel.
Most people reading Matthew 1 today don't see the relevance - even taking into consideration that Matthew was demonstrating Jesus' validity as a Jew. However, Matthew was also demonstrating a key point: God always keeps His promises. God had made promises to a number of people in the Old Testament, that one day, their descendant would be the Messiah.
Let's look at a few examples:
Abraham
Genesis 12 v 2-3
'I will make of thee a great nation, and I will bless thee, and make thy name great; and thou shalt be a blessing: And I will bless them that bless thee, and curse him that curseth thee; and in thee shall all families of the earth be blessed'. Judah
Genesis 49:8-10
"Judah, your brothers will praise you; your hand will be on the neck of your enemies;
your father’s sons will bow down to you.
You are a lion’s cub, Judah; you return from the prey, my son.
Like a lion he crouches and lies down, like a lioness—who dares to rouse him?
The sceptre [a symbol of royalty] will not depart from Judah,
nor the ruler’s staff from between his feet, until he to whom it belongs shall come"
David
2 Samuel 7:16
"Your house and your kingdom will endure forever before me; your throne will be established forever."
And another more obscure member of Jesus' ancestors:
Zerubbabel (Matthew 1:12. Zerubbabel led the work on the reconstruction of Jerusalem from the rubble that was left when the Israelites returned from their exile)
Haggai 2:20-23
20 The word of the LORD came to Haggai a second time on the twenty-fourth day of the month: 21“Tell Zerubbabel governor of Judah that I am going to shake the heavens and the earth. 22 I will overturn royal thrones and shatter the power of the foreign kingdoms. I will overthrow chariots and their drivers; horses and their riders will fall, each by the sword of his brother.
23 “‘On that day,’ declares the LORD Almighty, ‘I will take you, my servant Zerubbabel son of Shealtiel,’ declares the LORD, ‘and I will make you like my signet ring, for I have chosen you,’ declares the LORD Almighty.”
The signet ring in Old Testament times was a royal symbol. A signet, engraved with the king's seal, was used to endorse official documents. To guard against misuse, the king wore it as a ring or on a necklace. God declares here that He's chosen Zerubbabel and would keep him safe to fulfil his appointed purpose; since this didn't happen during his lifetime, we can see that this would extend to one of his descendants... and sure enough...
There are quite a few other interesting characters in Matthew 1... and I like to think of it as a roll of honour.
Thursday 2 February 2012
Probabilities and Free Toys: Part Four
Well, after all the work I've done on probabilities and free toys in 'blind' packaging, such as cereal packets, or toy action figures, it seems like I've missed a neat little trick. I was reading a maths puzzle in a book a few days ago about this exact problem! The book in question is called Math-E-Magic, by Raymond Blum, Adam Hart-Davis, Bob Longe and Derrick Niederman.
I couldn't quite believe my luck... and then felt slightly deflated, when I reflected on all the number-crunching that I've done so far, and how I did not see this alternative approach (although it doesn't give the same degree of detail in its solution).
The puzzle is posed thus: "Cereal Serial: A cereal company places prizes in its cereal boxes. There are four different prizes distributed evenly over all the boxes the company produces. On average, how many boxes of cereal would you need to buy before you collected a complete set?"
This is a slightly different approach than I've been using (how many boxes to achieve 90% probability of getting a full set), which makes the maths easier, but the solution - one 'average' figure - gives no indication of the spread of results, which I achieved previously.
The answer, however, is elegantly simple.
To obtain the first toy, we need to buy just one box, as we are guaranteed to get a toy we haven't had before.
For the second toy: we have a probability of 3/4 of getting a new toy in the second box. Therefore (and this is a big therefore which will need explaining separately), it'll take on average 4/3 boxes to obtain a new toy.
For the third toy, the probability of getting a new toy is 2/4 or 1/2, and therefore it will take an average of 2 boxes to get a toy we haven't had before.
And finally, for the fourth toy, the probability of getting a new toy is 1/4, and it will therefore take four additional boxes to get the final toy.
So, the average number of boxes it will take to get the four toys is:
1 + 4/3 + 2 + 4 = 8 1/3
To quote the answers from Mathemagic: "In real life, of course, you can't buy 1/3 of a box, but that is still the average number of boxes you'd have to purchase."
As I said, I'm not familiar with the approach of taking reciprocals to obtain "number of boxes" from probabilities, although it seems intuitive. I must have missed that lesson at school! Let's take a look at it a little more closely.
If an event has a 1/4 probability of success, then how many times do I have to repeat it, on average, to achieve one success? It seems overly simple to say "Four times" but that appears to be the answer - certainly, the answer given in Mathemagic works on this principle. And logically, it makes sense. If we were to try to measure the probability of a success event (without knowing what the probability was) then we'd take the number of successes and divide by the number of attempts. If we were successful once in four tries, then p(success) = 1/4. And on average, working backwards to reach the answer we're looking for, we'd expect one success in four attempts. I will bear all this in mind next time I find a free toy inside a cereal packet... especially if it's one of a set of 16!
Let's take a look at the results from last time, and see if they can be used to confirm or support this calculation.
Firstly, here are the results with number of tries along the x-axis, and probability of success on the y-axis. Each line represents a different number of toys in the set (two toys on the left, ten toys is the right-most).
Let's take a look at the slopes for each graph - to make things easier to see, let's just look at the cases t = 2, 3, 4 and 5.
Here are the graphs of dp/dn or how the gradients of the graphs above change with number of tries. As I pointed out last time, the graphs have a region of maximum slope - where the probability of getting the full set of toys rises most sharply. This is the region where we will approach the average number of boxes we need to buy, so, by finding the slope of the graph (in this case I've just subtracted adjacent figures to determine the change in probability, since I haven't got the actual function to differentiate).
What does this show us? For toys=2, maximum slope is at n=2 (where the probability goes from zero to 50%), but the more meaningful result is at n=3 where the probability goes from 50% to 75%. Beyond this, the slope tails off very quickly.
This result also matches the formulaic approach shown above:
Probability of 'new' toy with one box = 1 so 1/1 =1 number of boxes to be bought.
Probability of 'new' toy with second box = 1/2, so 1/ (1/2) = 2 boxes to be bought.
1+2 = 3
Average number of boxes for a two-toy set is three boxes.
Let's re-examine t=4, which we discussed at the start of this post. My results graph shows a peak around n=7~8 which is in good agreement with the arithmetic figure of 8 1/3. I'm not sure if this validates my method or the solution :-) but it's good to see some agreement between practical experiment and calculated figures.
Finally, let's look at t=5, the purple line on my graph.
Mathematically, the average number of boxes will be:
1 + 1 1/4 + 1 2/3 + 2 1/2 + 5 = 11 5/12 or just under 11.5 boxes (11.41667).
However, the peak for t=5 on my graph is at n=9 boxes, and this (along with the results for t=4) seem to suggest an oversimplification in the calculated method that I've been using. I just can't quite put my finger on it, or explain it clearly and concisely!
Perhaps I've made a mistake in the analysis of my data. Recalling my maths lessons at school, I suspect that the 'average' number of boxes is obtained when the probability of collecting the full set of toys is equal to (or slightly greater than) 50%.
Reviewing my data, this gives:
Which still shows an over-estimation by the arithmetic method (or an over-achievement by the modelling approach). Consequently, I still feel a little concerned with the arithmetic method. I think it's related to the probability of getting a new toy when you've already collected half the set and you're starting to get fewer successful 'new' toys, but I can't quite identify if there's a flaw in the model or in my results. I would leave it as: when you come to find the final toy in a set of five, having already bought six boxes for the first four, is it really going to take FIVE more boxes? Somehow, that doesn't feel right (although, as I've read previously, human beings are very poor judges of probability).
I'd really like to reach closure with this puzzle... I think I may take the mathematical approach for now, and re-examine my data at a later time!!
Labels:
maths,
probability,
problem,
puzzle
Subscribe to:
Posts (Atom)